코드메모장

(1) 문제

• 베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다.
• 이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼프가 1850년에 증명했다.
• 예를 들어, 10보다 크고, 20보다 작거나 같은 소수는 4개가 있다. (11, 13, 17, 19) 또, 14보다 크고, 28보다 작거나 같은 소수는 3개가 있다. (17,19, 23)
• 자연수 n이 주어졌을 때, n보다 크고, 2n보다 작거나 같은 소수의 개수를 구하는 프로그램을 작성하시오. 

(2) 입력

• 입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 케이스는 n을 포함하는 한 줄로 이루어져 있다.
• 입력의 마지막에는 0이 주어진다.
• 1 ≤ n ≤ 123,456

(3) 출력

• 각 테스트 케이스에 대해서, n보다 크고, 2n보다 작거나 같은 소수의 개수를 출력한다.

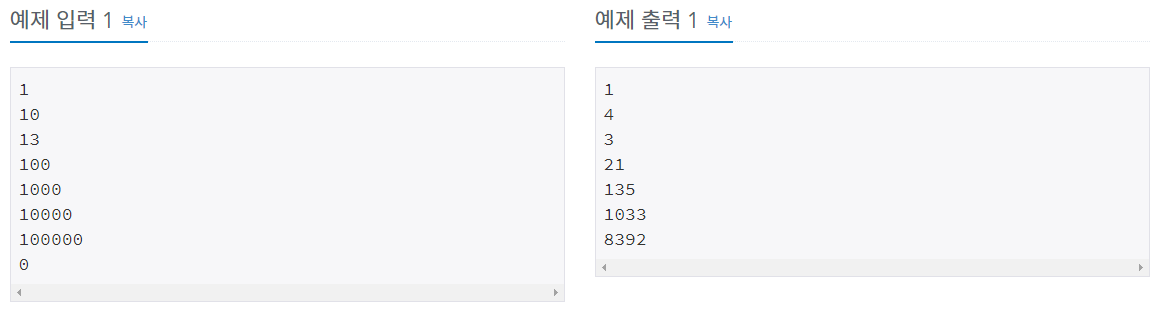
(4) 예제 입력 및 출력

(5) 코드

• n이 123456 이하로 제한되어 있어 소수를 미리 구하고 비교

import sys
import math

prime = []

for i in range(2, (123456 * 2) + 1):
    prime_check = True
    #제곱근 구하기
    sqrt_number = int(math.sqrt(i + 1))
    for j in range(2, sqrt_number + 1):
        if i % j == 0:
            prime_check = False
            break
    if prime_check:
        prime.append(i)

while True:
    number = int(sys.stdin.readline())
    count = 0
    if number == 0:
        break

    for element in prime:
        if element > number:
            if element <= number * 2:
                count += 1
            else:
                break
    
    print(count)

• 글자수 사이의 소수를 실시간으로 구하기(python3로 하면 시간초과 pypy통과)

import math
import sys

while True:
    number = int(sys.stdin.readline())
    if number == 0:
        break
    min_number = number + 1
    max_number = number * 2

    prim_count = 0

    for i in range(min_number, max_number + 1):
        prime_check = True
        #제곱근 구하기
        sqrt_number = int(math.sqrt(i + 1))
        for j in range(2, sqrt_number + 1):
            if i % j == 0:
                prime_check = False
                break
        if prime_check:
            prim_count += 1

    print(prim_count)

(6) 실행결과

(1) 문제

• 우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행사가 되어 새로운 세계에 발을 내려 놓는 영광의 순간을 기다리고 있다.
• 그가 탑승하게 될 우주선은 Alpha Centauri라는 새로운 인류의 보금자리를 개척하기 위한 대규모 생활 유지 시스템을 탑재하고 있기 때문에, 그 크기와 질량이 엄청난 이유로 최신기술력을 총 동원하여 개발한 공간이동 장치를 탑재하였다. 하지만 이 공간이동 장치는 이동 거리를 급격하게 늘릴 경우 기계에 심각한 결함이 발생하는 단점이 있어서, 이전 작동시기에 k광년을 이동하였을 때는 k-1 , k 혹은 k+1 광년만을 다시 이동할 수 있다. 예를 들어, 이 장치를 처음 작동시킬 경우 -1 , 0 , 1 광년을 이론상 이동할 수 있으나 사실상 음수 혹은 0 거리만큼의 이동은 의미가 없으므로 1 광년을 이동할 수 있으며, 그 다음에는 0 , 1 , 2 광년을 이동할 수 있는 것이다. ( 여기서 다시 2광년을 이동한다면 다음 시기엔 1, 2, 3 광년을 이동할 수 있다. )

• 김우현은 공간이동 장치 작동시의 에너지 소모가 크다는 점을 잘 알고 있기 때문에 x지점에서 y지점을 향해 최소한의 작동 횟수로 이동하려 한다. 하지만 y지점에 도착해서도 공간 이동장치의 안전성을 위하여 y지점에 도착하기 바로 직전의 이동거리는 반드시 1광년으로 하려 한다.
• 김우현을 위해 x지점부터 정확히 y지점으로 이동하는데 필요한 공간 이동 장치 작동 횟수의 최솟값을 구하는 프로그램을 작성하라.

(2) 입력

• 입력의 첫 줄에는 테스트케이스의 개수 T가 주어진다. 각각의 테스트 케이스에 대해 현재 위치 x 와 목표 위치 y 가 정수로 주어지며, x는 항상 y보다 작은 값을 갖는다. (0 ≤ x < y < 231)

(3) 출력

• 각 테스트 케이스에 대해 x지점으로부터 y지점까지 정확히 도달하는데 필요한 최소한의 공간이동 장치 작동 횟수를 출력한다.

(4) 예제 입력 및 출력

(5) 코드

import math
import sys
length = int(sys.stdin.readline())

for i in range(length):
    date_conut = 0
    x, y = sys.stdin.readline().split()
    x = int(x)
    y = int(y)
    distance = y - x
    if distance <= 3:
        print(distance)
    else:        
        square_root = int(math.sqrt(distance))
        
        if distance == square_root ** 2:
            date_conut = 2 * square_root - 1
        elif distance > square_root ** 2  and distance <= square_root ** 2 + square_root:
            date_conut = 2 * square_root
        else:
            date_conut = 2 * square_root + 1    
        print(date_conut)

(6) 실행결과

(1) 문제

• 상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그램 봉지와 5킬로그램 봉지가 있다.
• 상근이는 귀찮기 때문에, 최대한 적은 봉지를 들고 가려고 한다. 예를 들어, 18킬로그램 설탕을 배달해야 할 때, 3킬로그램 봉지 6개를 가져가도 되지만, 5킬로그램 3개와 3킬로그램 1개를 배달하면, 더 적은 개수의 봉지를 배달할 수 있다.
• 상근이가 설탕을 정확하게 N킬로그램 배달해야 할 때, 봉지 몇 개를 가져가면 되는지 그 수를 구하는 프로그램을 작성하시오.

(2) 입력

• 첫째 줄에 N이 주어진다. (3 ≤ N ≤ 5000)

(3) 출력

• 상근이가 배달하는 봉지의 최소 개수를 출력한다. 만약, 정확하게 N킬로그램을 만들 수 없다면 -1을 출력한다.

(4) 예제 입력 및 출력

(5) 코드

import sys

FIVE = 5
THREE = 3

sugar = int(sys.stdin.readline())

min_x = sugar // FIVE
min_y = (sugar - (FIVE * min_x)) // THREE

while True:
    if min_x * FIVE + min_y * THREE == sugar:
        print(min_x + min_y)
        break
    else:
        min_x -= 1
        min_y = (sugar - (FIVE * min_x)) // THREE

    if min_x == -1:
        print(-1)
        break

(6) 실행결과