728x90
(1) 문제
- 방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
(2) 입력
- 첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
(3) 출력
- 첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.
(4) 예제 입력 및 출력
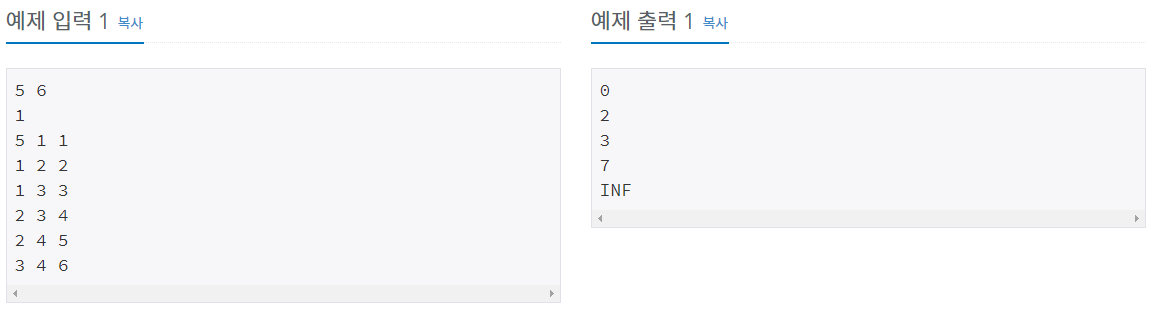
(5) 코드
import heapq
import sys
point_count, line_count = sys.stdin.readline().split()
point_count = int(point_count)
line_count = int(line_count)
start_point = int(sys.stdin.readline())
line_dic = {}
for i in range(point_count):
line_dic[i + 1] = []
for i in range(line_count):
u, v, w = sys.stdin.readline().split()
line_dic[int(u)].append((int(v),int(w)))
def dijkstra(graph, start):
distances = {node + 1: float('inf') for node in range(point_count)}
distances[start] = 0
queue = []
heapq.heappush(queue, [distances[start], start])
while queue:
# print(f'distances = {distances}')
# print(f'queue = {queue}')
current_distance, current_node = heapq.heappop(queue)
if distances[current_node] < current_distance:
continue
for line in graph[current_node]:
adjacent = line[0]
weight = line[1]
distance = current_distance + weight
if distance < distances[adjacent]:
distances[adjacent] = distance
heapq.heappush(queue, [distance, adjacent])
return distances
distance_dic = dijkstra(line_dic, start_point)
for value in distance_dic.values():
if value == float('inf'):
print('INF')
else:
print(value)(6) 실행결과

반응형
'BaekJoon Algorithm > Python' 카테고리의 다른 글
| [백준알고리즘 - 2667] 단지번호붙이기(Python) (0) | 2021.04.11 |
|---|---|
| [백준알고리즘 - 11054] 가장 긴 바이토닉 부분 수열 (Python) (1) | 2021.04.11 |
| [백준알고리즘 - 1992] 쿼드트리 (Python) (0) | 2021.04.11 |
| [백준알고리즘 - 2231] 요세푸스 문제 0 (Python) (0) | 2021.03.28 |
| [백준알고리즘 - 2231] 분해합 (Python) (0) | 2021.03.28 |